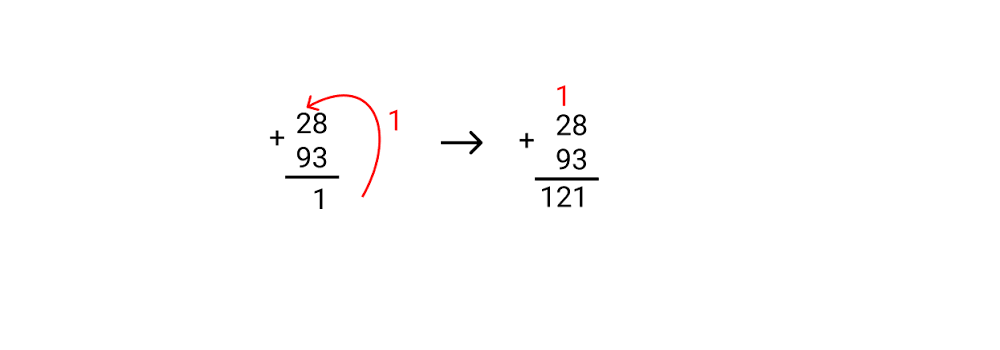
De início, achei a ideia desse texto bastante pueril, mas decidi compartilhar com vocês alguns dos meus devaneios dessa semana depois de ler uns tweets da Julia Jaccoud (a Matemaníaca) sobre as descobertas de seus alunos.

Vocês já se perguntaram de onde vêm aquelas regras de adição de números com mais de um algarismo? Sabe, aquele “Sobe um”, “Vai dois”, essas coisas que surgem quando nós somamos 18 com 17, por exemplo. Eu confesso que pouco parei para pensar nisso na vida, pelo menos que eu me lembre, mas me peguei pensando nisso esses dias. Gosto de fazer isso, pensar sobre as bases “simples” do conhecimento comumente ensinado.

Vamos lá então?!

Cês já tentaram somar 18 com 17?

Figura 1: Conta armada da soma de 18, em cima, com 17, em baixo, tendo como resultadoo valor 35.

Como eu aprendi lá na alfabetização (atual primeiro ano do ensino fundamental), somam-se os algarismos de cada coluna indo da direita para esquerda, logo teremos que 8+7 é 15, como 15 não cabe ali em baixo, nós subimos o 1 para outra coluna e então somamos normalmente todos os algarismos naquela coluna, que, agora são três.

Mas por que o 15 não cabe ali em baixo?

Pensando nisso, como era assunto de alfabetização, lembrei de outra coisa que aprendi naquela época: unidades, dezenas, centenas, unidades de milhar e por aí vai. Essa era a resposta e justificava, até mesmo as regras das outras operações.

Figura 2: Imagem de um exercício para crianças colocarem os números indicados com suas respectivas centenas, dezenas e unidades. Os número são 235, 35, 106 e 407. Fonte

Vamos relembrar os conceitos caso não se lembre. Afinal, mesmo para mim, já fazem uns 20 anos.

Quando escrevemos um número, ou pelo menos aquilo que é comumente aceito pelas pessoas como um número, podemos compartimentá-lo em unidades, dezenas, centenas e por vai. Para exemplificar de forma simples, eu vou usar a última imagem, agora respondendo esse exercício.

Figura 3: Assim, como a figura 2, contudo, respondida.

Se pegarmos o primeiro exemplo, o número 235, vemos que ele tem duas centenas, três dezenas e cinco unidades, contudo, podemos dizer também que ele tem vinte e três dezenas e cinco unidades ou mesmo dizer que ele tem duzentos e trinta e cinco unidades (sim, também podemos dizer que ele tem duas centenas e trinta e cinco unidades, ou qualquer outro arranjo possível). Essa compartimentação serve para nos indicar um peso associado a cada algarismo. Veja o caso do dois no número 235, 2 é menor que 5, contudo o número dois nesse número está relacionado as centenas, então este número dois é maior que o número cinco que está relacionado somente às unidades. Isso pode parecer simplista e intuitivo (e tomara que seja mesmo), mas, olhando mais a fundo, isso está relacionada diretamente ao sistema de bases que usamos para os números e é uma grande conquista dos numerais indo-arábicos sobre os romanos e os semíticos.

Considere o número 47₈ em base octal. Nesse número o algarismo oito significa oito mesmo, mas o algarismo quatro significa 4 vezes 8 que é 32. Embora 4 ainda seja menor que 8 nesse sistema, ele, agora, significa 32, não mas 40 (quatro dezenas) da base decimal. Se escrevermos 47 em algarismos romanos, por exemplo (afinal eu não sei hebraico), escreveríamos como XLVII, nesse sistema X é dez, e embora ele esteja a frente do L, que é o símbolo para cinquenta, ele não significa um número maior como cem, ele significa dez mesmo, mas uma subtração de forma de XL é 50-10 , ou seja, 40, enquanto LX é 50+10, ou seja, 60. Aqui, a posição não indica mais um valor em si. O valor dos algarismos continua o mesmo e sua posição pode indicar uma operação a ser realizada.

Como eu falei há três parágrafos atrás, essas questão da posição dar um significado maior ao número, como o de unidades, dezenas e tal, é a resposta para porque sobe 1. Vamos armar a conta de 18+17, agora posicionando e identificando em unidades e dezenas.

Figura 4: Conta armada indicando dezenas e unidades dos componentes da soma de 18, em cima, com 17, em baixo, tendo como resultado o valor 35.

Mais uma vez, quando somamos 8 unidades mais 7 unidades, obtemos 15 unidades, logo, uma dezena e 5 unidades. Desta forma, aquele 1 “sobe” por simbolizar um dezena e digo “sobe” com aspas, pois isso é uma questão se simbolismo para nos ajudar  a organizar uma operação (a adição) que sabemos como funciona. Nós podemos, inclusive, utilizando as propriedades de adição que eu mostrei em outro texto, armar essa conta de maneira que não se suba nenhum novo algarismo.

Se armarmos essa conta, teremos uma adição que não vai adicionar nenhum valor novo na “casa das dezenas” (Como dizia a Tia Rose <3)

Figura 5: Conta armada indicando dezenas e unidades dos componentes da soma de 20, em cima, com 15, em baixo, tendo como resultado o valor 35.

Como falei, isso também explica o “empresta” da subtração. Façamos um exemplo,

Figura 6: Conta armada indicando centenas, dezenas e unidades dos componentes da diferença entre 901, em cima, com 118, em baixo, tendo como resultado o valor 783.

Nesse caso, temos mais etapas, mas o princípio é o mesmo. Temos que subtrair o algarismo 1 do 8, o que não é possível, então transformar uma dezena em 10 unidades, contudo o algarismo que está na casa das dezenas é o 0, logo, não temos dezenas disponíveis, então vamos transformar uma centena em dez dezenas. Fazendo isso, as 9 centenas passam a ser 8 e, agora temos 10 dezenas ao invés de 0, então transformamos uma dezena em 10 unidades, passando então a ter 9 dezenas e 11 unidades, como 11 é maior que 8, podemos fazer a subtração normalmente 11-8 é 3, aquelas 10 dezenas, agora são 9, então 9-1 é 8 e as 9 centenas são 8, então temos que 8-1 é 7.

Mas não é só apenas isso (como diria o seu Casseta), nós, podemos , com isso explicar a multiplicação também. Peguemos o exemplo que eu montei.

Figura 7: Conta armada da multiplicação entre 33, em cima, com 14, em baixo, tendo como resultado o valor 462.

Fazendo a multiplicação como aprendemos no fundamental, temos 4 multiplicando o 3, da casa das unidades, o que resulta em 12, como sabemos, ficamos apenas com o 2 na parte das unidades e subimos com o 1, então multiplicamos 4 com 3, agora o 3 da casa das dezenas, o que nos resulta em 12 também e somamos esse valor, 12, com o 1 que subiu. Isso pois, o que temos aqui são 12 dezenas, visto que temos a multiplicação de 4 por 3 dezenas, como somamos dezenas com dezenas, então somamos essas 12 dezenas com a outra dezena que “subiu”, tendo , por fim o número 132. Quando fazemos a multiplicação do 1 pelo 33, não há dificuldade, pois 1 vezes qualquer coisa é qualquer coisa. Contudo, temos uma pequena regra, de que os valores que saem essa multiplicação “pulam uma casa” quando colocados abaixo do 132, o resultado da primeira multiplicação, como eu disse, isso agora é explicado pois aquele 1, simboliza uma dezena inteira, logo o que temos fazendo a multiplicação do algarismo 1, do número 14, pelo 33, é o valor de 33 dezenas, ou seja, 330. Então, “pulamos uma casa” quando escrevemos o valor dessa multiplicação, pois a casa das unidades, nessa parte da conta é ocupada pelo valor zero, sempre, pois vem da multiplicação de uma dezena por um número e o mesmo vai ocorrer com as centenas, que nos diziam para pular duas casas e os milhares e assim por diante.

Como eu falei, isto está ligado, de forma mais profunda, com o nosso sistema numérico, de modo que isso pode ser também aplicado a outros. Vamos pegar o velho exemplo da base octal.

Figura 8: Conta armada da soma entre 228, na base octal, em cima, com 178, na base octal, em baixo, tendo como resultado o valor 418.

Assim, somamos normalmente. Como a base é octal, quando somamos 2₈+7₈, não temos 9₈ e sim 11₈, pois o algarismo 9 não existe nessa representação, por isso, é costume indicar a base com um número subscrito indicando, nesse caso, eu utilizei o 8, de base octal. Como falei, utilizando o mesmo conceito, conseguimos entender isso, agora não temos mais dezenas e sim uma “octena” assim por dizer, de modo que os algarismo mais a esquerda serão multiplicados por potências de 8, como 8, 64, 512, e não mais por potências de 10, como 10, 100, 1000.

É só isso por hoje galerinha, espero que tenham gostado desse texto um tanto mais para ensino fundamental. Se você tiver o mesmo grau de escolaridade que eu, dificilmente vai utilizar isso, a menos que seja professor, mas fica como curiosidade.

Bye bye.