Sim, caros leitores, volto para a divagação sobre a crise existencial da física teórica.

No meu último texto parei nos anos 80, quando tínhamos 5 teorias de supercordas diferentes. Enorme problema para aquela que se propunha a ser a teoria de tudo.

Porém, em 1987, o fisico Balachandran Sathiapalan que, além de ter um nome muito legal, publica um artigo que começa a mudar toda a história. Nele é proposto (de forma simplista) algo pouco usual. Imagine uma teoria de cordas (daquelas que exemplifiquei nesse texto). Balachandran descreveu da mesma forma, com uma diferença: o espaço-tempo em que essas cordas se movem é circular. Sim, você leu certo, um círculo! Lembra daquela cena de Matrix em que Neo está preso em uma estação de metrô? Aí ele corre para dentro do túnel, quando ele chega ao fim, volta ao começo, lembra?

Em matemática dizemos que o espaço que ele vivia tem a topologia de um círculo, pois, assim como um círculo, o começo e o fim estão conectados no mesmo ponto.

Bom, Balachandran (sim, vou repetir pq adorei esse nome mesmo!) percebeu que, quando assumimos isso para uma teoria de cordas, é a mesma coisa de imaginar a mesma coisa para um círculo com o inverso do raio.

Não entendeu P. nenhuma, certo?

Vamos lá, porque isso é realmente estranho e desafia algumas noções de realidade. O que estamos dizendo aqui é o seguinte (momento do experimento mental):

Imagine que o espaço-tempo que você vive tem topologia de um círculo de raio de 1km. Isso quer dizer que no seu espaço-tempo, quando vc andar em linha reta para frente, ao andar 1km, vc volta ao começo.

Tudo certo até aqui? Não desista, vai ficar ainda mais maluco! Dado isso então, o que a teoria de Balachandran diz é que morar nesse espaço é a mesma coisa que viver em um espaço tempo com topologia de círculo, porém com um raio de 1 mm.

Isso, exatamente, eu consegui! Você está oficialmente maluco! Eu avisei que teoria de cordas era tão forte quanto ácidos dos anos 60.

Mas o que significa quando digo que morar em um círculo de 1 km é equivalente a morar em um círculo de 1mm? Ora, estou dizendo que a física, as partículas que essa teoria de cordas produz, é a mesma nos dois espaços. A física é a mesma, não faz diferença modelar em um ou no outro.

O que podemos tirar dessa loucura?

Primeiro que, quando estamos trabalhando com teorias desse tipo, nossos conceitos geométricos de distância se perdem. Segundo, duas teorias que parecem tão diferentes, acabam sendo equivalentes. Estão entendendo onde quero chegar? Se não entendeu, fique calmo que vamos chegar lá.

O nome dado a essa equivalência foi Dualidade T. Vale notar aqui que na época existia uma outra equivalência entre teorias, a dualidade S. Em eletrodinâmica, quando trocamos o campo elétrico pelo magnético e vice-versa, temos os mesmos resultados. Eletromagnetismo trata disso. Campos elétricos e magnéticos fazem parte de uma mesma estrutura.

Por que estou falando sobre isso?

É meio que a realização do maior sonho de Einstein, unificar a física em uma só teoria, uma equação que explique tudo o que conhecemos. Unificar diferentes verdades em um mesmo princípio é o máximo que a física fundamental pode chegar.

Lembra do nosso problema em ter 5 teorias de cordas diferentes?

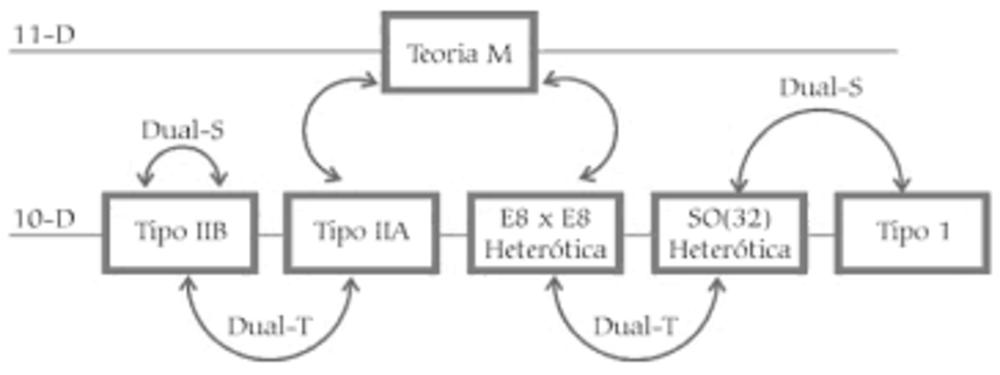
Tipo I, IIA, IIB, e as heterótica: E8xE8 e SO(32). Mais uma vez, nomes ótimos!

Em 1994, o físico Ashoke Sen propôs que a teoria tipo I é equivalente à teoria heterótica SO(32) pela dualidade S. Fantástico, não? Usando uma dualidade, ele diminuiu de 5 pra 4 teorias de cordas. Com a dualidade T foi possível mostrar ainda que as teorias IIA e IIB são equivalentes entre si e as duas heteróticas também. Com isso, de 5 teorias baixamos para duas.

Em 1995, um sujeito nada desconhecido no meio, Edward Witten, já havia ganhado a medalha fields (nobel da matemática) em 1990. Em uma palestra em um evento, conjecturou que deve existir uma teoria com 11 dimensões que ligaria todas as 5 teorias de cordas.

Um ano depois ele publicou junto com Petr Horava o trabalho que dá início aos desenvolvimentos da teoria M, até hoje inacabada. Como ainda não cumpriu seu principal papel, unificar as teorias de cordas e se transformar na teoria de tudo, muitas pessoas não acreditam que essa teoria um dia vai alcançar seu objetivo.

Bom, isso parece algo do tipo de um anticlímax, as dualidades resolveram o problema pela metade. Será que isso vai tornar todo esse estudo em cordas um exercício supérfluo?

Se a busca for somente pela teoria de tudo, pode-se dizer que está em desenvolvimento ainda, não com tanto vigor quanto a 20 anos, mas ainda trabalhando nisso.

Se você está buscando algo mais aplicado, mais prático, isso sim está fervendo! Não no sentido de estarmos desenvolvendo experimentos para detectar cordas, isso está muito, muito, muito longe. O artigo de Horava-Witten serviu para talvez o maior desenvolvimento em física teórica nos últimos anos:

A conjectura AdS/CFT.

E isso meus amigos, é física da pesada!

Se preparem para os próximos textos que essa brisa está longe de passar…