Oi, sou o Léo.

Na parte 1 exploramos o que é metrologia e falamos de metrologia clássica, que lida com medida macroscópicas. Agora vamos abordar a metrologia quântica, que se aventura no reino subatômico da matéria.

Metrologia Quântica: E agora, José?

Agora que exploramos a metrologia clássica, é hora de dar uma olhada na metrologia quântica. Esta é uma área empolgante da metrologia que lida com medidas em escalas subatômicas, em que as partículas se comportam de maneira completamente diferente daquilo que estamos acostumados a ver no mundo macroscópico (para ver alguns trabalhos do carinha que escreve aqui, vá nas referências).

A metrologia quântica nos leva ao reino subatômico, onde as partículas, como elétrons e fótons, exibem comportamentos quânticos, incluindo superposição e emaranhamento.

Quando tentamos medir propriedades quânticas, somos levados necessariamente a lidar com coisas “bizarras” como o princípio da incerteza de Heisenberg, que nos diz que não podemos conhecer simultaneamente com precisão a posição e a velocidade de uma partícula, por exemplo. Em vez disso, entramos no mundo das distribuições de probabilidade, pois a Teoria Quântica é intrinsecamente probabilística.

Princípio da Incerteza de Heisenberg

O princípio da incerteza de Heisenberg é um dos pilares da mecânica quântica e tem implicações profundas para a metrologia quântica. A equação do princípio da incerteza de Heisenberg é dada por:

Δx⋅Δp≥2ℏ

Δx representa a incerteza na posição da partícula, Δp representa a incerteza na sua momento (massa vezes velocidade) e ℏ é a constante de Planck reduzida, que é uma constante fundamental da física quântica.

Essa equação nos diz que quanto mais precisamente medimos a posição de uma partícula, menos precisamente podemos conhecer, simultaneamente, sua velocidade, e vice-versa. Essa é uma limitação intrínseca da natureza quântica do mundo.

Teoria de Estimativas Quânticas

Na metrologia quântica, a teoria de estimativas é baseada em probabilidades, superposição e emaranhamento. Quando medimos uma propriedade quântica, não obtemos um valor determinístico, mas sim uma distribuição de probabilidade que nos diz a probabilidade de encontrar a partícula em diferentes estados. Isso é uma consequência direta do princípio da incerteza de Heisenberg e de características como superposição, emaranhamento, etc.

Em teoria de estimativas quânticas também temos um limite, tipo o de Cramer-Rao citado acima, mas usando H(θ), que é a Informação de Fisher quântica. É interessante notar que usando sistemas quânticos é possível, em algumas das vezes, obter uma precisão MAIOR que usando sistemas clássicos, o que é da hora demais.

Uso da Luz Comprimida no LIGO para Medir Ondas Gravitacionais

Além das aplicações da metrologia clássica e quântica em escalas conhecidas, há também aplicações avançadas que exploram os princípios da mecânica quântica em escalas macroscópicas para alcançar medições extremamente precisas. Um exemplo notável disso é o uso da luz comprimida no Laser Interferometer Gravitational-Wave Observatory (LIGO) para detectar e medir ondas gravitacionais.

As ondas gravitacionais são perturbações no espaço-tempo que são geradas por eventos cósmicos cataclísmicos, como a colisão de buracos negros ou estrelas de nêutrons. Essas ondas se propagam pelo espaço-tempo e, quando atingem a Terra, causam pequenas deformações no espaço (!!!), que podem ser detectadas e medidas com grande precisão.

O LIGO é um experimento incrivelmente sensível que utiliza interferometria a laser para detectar ondas gravitacionais. Funciona da seguinte forma: um feixe de laser é dividido em dois ramos que percorrem caminhos perpendiculares entre si. Esses feixes de luz refletem-se em espelhos e, em seguida, retornam ao ponto de origem, onde são recombinados e depois detectados, onde apresentam claramente o que chamamos “franjas de interferência”.

Figura contendo explicações sobre o funcionamento do LIGO, conforme explicado acima.

Uma Figura animada (gif) contendo explicações sobre como um interferômetro, tipo o LIGO, funciona.

O princípio básico da interferometria é que, quando os dois feixes de luz retornam, eles podem estar em fase (pico com pico e vale com vale), resultando em uma intensidade máxima, ou fora de fase, resultando em uma intensidade mínima. Qualquer mudança no comprimento dos caminhos percorridos pelos feixes de luz causará uma mudança na intensidade medida.

O que torna o LIGO tão especial é sua incrível sensibilidade. Ele é capaz de medir deformações no espaço-tempo da ordem de uma fração do tamanho de um núcleo atômico!

O LIGO está, desde pouco tempo pra cá, usando o que chamamos de “luz comprimida” para melhorar a precisão de suas medições. A “luz comprimida” é um tipo de luz que uma das quadraturas (chame por exemplo de Δx na equaçãozinha do princípio de incerteza) é… comprimida… ao passo que outra quadratura, o Δp, é alargada.

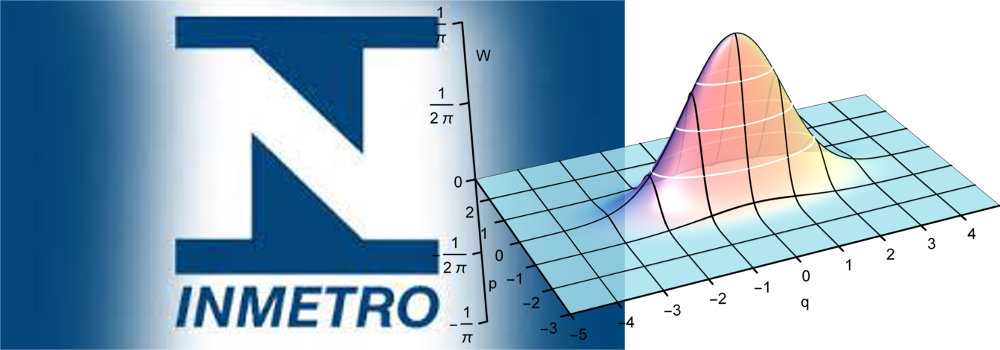
Gráfico da função de Wigner de um estado de Luz Comprimida. Repare que o que chamamos de quadratura p nesta figura é bem mais “magrinha” que a quadratura q. Portanto essa é uma Luz Comprimida.

O uso da luz comprimida no LIGO para detectar e medir ondas gravitacionais é um exemplo impressionante de como os princípios da metrologia quântica podem ser aplicados em escalas macroscópicas.

A capacidade do LIGO de medir deformações espaciais extremamente pequenas ilustra a combinação de física quântica e metrologia em ação. E o uso de Luz Comprimida, trazendo de fato recurso quântico para o LIGO, favorece a precisão de suas medições.

Concluindo

Em conclusão, a metrologia é uma ciência fascinante que nos permite medir e compreender o mundo em todas as suas escalas. Na metrologia clássica, usamos instrumentos para fazer medições precisas em escalas macroscópicas, como peso e temperatura. A teoria de estimativas clássicas, incluindo o Limite de Cramér-Rao Clássico, nos ajuda a entender a incerteza associada a essas medidas.

Por outro lado, na metrologia quântica, entramos no mundo subatômico, onde as leis da mecânica quântica governam o comportamento das partículas. A teoria de estimativas quânticas nos ensina a lidar com essa incerteza e a interpretar medidas probabilísticas. E o uso de propriedades genuinamente quânticas pode permitir um aumento na precisão de medições.

A metrologia é uma área em constante evolução, e sua importância vai além da nossa vida cotidiana, sendo fundamental para o avanço da ciência e da tecnologia. Ela nos ajuda a explorar os limites do conhecimento e a compreender o mundo em todas as suas complexidades, desde as maiores escalas até as menores, onde as equações e os princípios da metrologia clássica e quântica nos guiam em nossa busca pelo entendimento.

É isso por hoje.

Forte abraço,

Leo.

Referências:

[1] Tese de Doutorado de Leo. Souza: http://hdl.handle.net/1843/ESCZ-7ZFGKK

[2] Alguns artigos sobre metrologia quântica:
https://arxiv.org/abs/1703.05554
https://arxiv.org/abs/0807.3958