Em tempos antigos, quando não havia uma rede eficiente de transportes entre diferentes cidades, eram os caixeiros viajantes que percorriam diferentes cidades para comercializar produtos não disponíveis em diferentes comunidades. No Brasil o termo mais comum é mascate. Quem não fugiu das aulas de história já ouviu falar da Guerra dos Mascates no Recife. Neste caso específico, os nobres do açúcar de Olinda alcunharam os comerciantes de Recife de mascates.
Caixeiros viajantes tinham uma difícil jornada e lidavam com decisões complexas. Compravam mercadorias onde existia grande oferta e serviam povoados em que os mesmos produtos não chegavam. Dentre as decisões que eles deveriam tomar, incluem-se: quais produtos e que quantidade comprar, o preço a ser vendido para cada freguês e que trajeto tomar. Provavelmente eles tomavam estas decisões baseados na experiência.
Com a decolada do método científico, problemas similares aos do caixeiros viajantes começaram a ser sistematicamente estudados e problemas como o do exemplo acima foram matematicamente formalizados. Estes problemas são comumente referidos com nomes específicos e nestes incluem o problema do caixeiro viajante e outro é o problema da mochila.
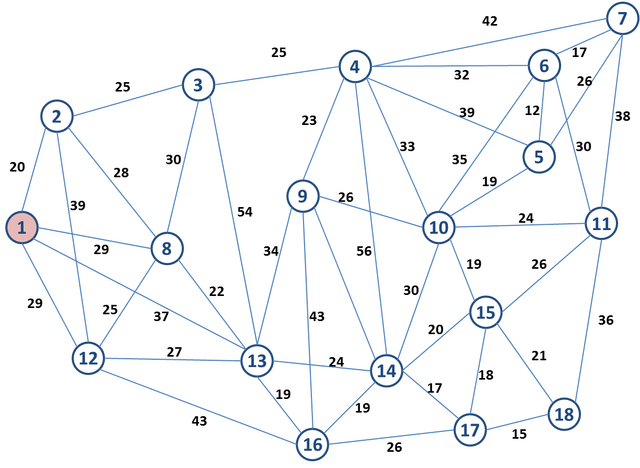
O problema do caixeiro viajante se refere a redução de custos de transporte (mas que pode ser visto como maximização de lucros). Digamos que o caixeiro viajante sabe todos os povoados que ele tem que visitar, as distâncias entre eles, a quantidade que ele vai vender e a que preço. Portanto ele já sabe o seu faturamento. Um caixeiro viajante sagaz deduziria que o objetivo dele é reduzir custos e ele pode fazer isso otimizando a rota que ele faz. Por exemplo, um caixeiro viajante que sai de Itajaí-SC (perto de Florianópolis) e tem que passar em São Paulo, Rio de Janeiro, Belo Horizonte, e Vitória saberia que seria contraproducente ele viajar a Belo Horizonte, retornar a São Paulo, depois ir ao Rio e a Vitória. No entanto, eu não saberia dizer de antemão se ele deveria ir a Vitória antes de Belo Horizonte ou o contrário. São algumas combinações possíveis, até podemos calcular a melhor rota com alguma paciência. Agora imagina se o caixeiro viajante tem que vender seus produtos em cada capital do Brasil? Existem milhares de combinações. Se minhas contas estão certas, seriam em torno de 4 sucedido de 26 zeros! O exemplo abaixo ilustra esse problema de visitar todas as capitais dos Estados Unidos cobrindo a menor distância possível.

Exemplo do problema do caixeiro viajante. Qual é a melhor sequencia de rota para visitar todas as capitais dos Estados Unidos? Retirado do post sobre o tema da Wikipedia
O problema da mochila se refere ao portfólio do caixeiro que modela a decisão do caixeiro com relação aos produtos que ele deve comprar e a quantidade. O caixeiro viajante tinha um limite físico da quantidade de mercadorias que ele poderia levar e tinha que considerar a obsolescência da mercadoria. Ele tinha que ser sagaz para saber o portfólio de produtos que maximizaria seus lucros. No entanto, o mesmo raciocínio serve para o exemplo anterior. Se ele vende dois tipos de tecido e um tipo de jóia ele consegue decidir facilmente. Mas como seria se ele tivesse que escolher para uma grande gama de produtos? Este problema é referido como “Problema da Mochila”. A figura abaixo ilustra a ideia do problema da mochila em que existe um peso máximo a ser levado e uma série de itens com diferentes valores e pesos. Temos que testar todas as combinações possíveis para assegurar que estamos carregando o máximo de valor possível.

Representação do problema da mochila. Retirado do verbete da Wikipedia sobre o mesmo assunto.
Com advento da ciência, em que avançamos? Sabemos que ainda não existe uma forma eficiente de resolver os dois problemas acima a não ser testando todas as combinações! É bem verdade que um computador pode testar muito mais combinações que o caixeiro viajante, mas para problema modestos como visitar todas as capitais é praticamente impossível testar todas as combinações com a tecnologia atual – diferentemente de outros problemas como, por exemplo, descobrir a rota de menor custo entre dois pontos em que há métodos eficientes para isso. Se você pedir para o Google te rotear do extremos sul ao extremo norte da América do Sul, o resultado sairá na tela em menos de 1 segundo.
Problemas com estruturas parecidas são conhecidos como “NP completos”, que em palavras simples são problemas difíceis de serem resolvidos e que ainda não conhecemos algoritmos eficientes para resolvê-los. A boa notícia é que esses diversos problemas têm estruturas parecidas e, se um dia um problema for resolvido eficientemente, todos os outros também serão.
É por isso que instituições como o Clay Math Institute (CMI) oferecem prêmios de 1 milhão de dólares se matemáticos provarem que existem métodos eficientes para estes problemas ou provarem o contrário – que não existe método algum que um dia possa resolver este problema. Este problema é um caso clássico em que a descoberta pode trazer ganhos bilionários no dia seguinte à descoberta. Afinal, isso tornará mais eficiente a operação de diversas indústrias como serviços de entrega (ótima rota), redes de supermercado (quais produtos colocar na “mochila”), empresas áreas (em que voo alocar cada funcionário), rotas de transporte público e outros mais. O caixeiro viajante ganharia 1 milhão, a humanidade pode ganhar bilhões.
Imagem de destaque retirado deste link que inclusive é um post interessante com mais detalhes da matemática do problema.
Verbete sobre Caixeiro-viajante Wikipedia
Verbete da Wikipedia sobre o problema do caixeiro viajante
Verbete da Wikipedia sobre o problema da mochila
Verbete da Wikipedia sobre problemas NP-Completos